Uji Hipotesis One Sample t Test Dengan SPSS – Metode Statistik
Inferensi merupakan metoda statistik yang digunakan untuk mengetahui
karakteristik sebuah populasi yang berjumlah banyak. Hal tersebut
berbeda dengan statistika deskriptif, yang digunakan untuk populasi yang
berjumlah sedikit. Statistika Inferensi dapat kita gunakan untuk
mengambil kesimpulan tentang keadaan sebuah populasi yang besar melalui
pengambilan sampel. Dalam metoda ini kita membutuhkan alat analisis
statistik yaitu Uji t, uji z, dan uji F.
One Sample t Test (Uji Satu Sampel), Pengujian ini dilakukan untuk menguji apakah suatu nilai tertentu yang digunakan sebagai pembanding berbeda secara signifikan dengan rata-rata sebuah sampel.
Dalam pengujian sampel ini, kita dapat menggunakan SPSS sebagai alat pengujian Hipotesis tersebut. Untuk latihan, berikut data-data yang bisa digunakan sebagai contoh.
Angaplah sebuah toko parfum membuat produk dengan isi 100 ml/botol. Lalu seorang karyawan toko tersebut ingin memastikan, apakah hal tersebut benar?. Karyawan tersebut menggunakan, 10 sampel parfum sebagai sampel yang akan diuji. berdasarkan hal tersebut, berikut data-data yang terkumpul.
Berdasarkan data tersebut, berikut langkah-langkah yang dapat kita lakukan.
One Sample t Test (Uji Satu Sampel), Pengujian ini dilakukan untuk menguji apakah suatu nilai tertentu yang digunakan sebagai pembanding berbeda secara signifikan dengan rata-rata sebuah sampel.
Dalam pengujian sampel ini, kita dapat menggunakan SPSS sebagai alat pengujian Hipotesis tersebut. Untuk latihan, berikut data-data yang bisa digunakan sebagai contoh.
Angaplah sebuah toko parfum membuat produk dengan isi 100 ml/botol. Lalu seorang karyawan toko tersebut ingin memastikan, apakah hal tersebut benar?. Karyawan tersebut menggunakan, 10 sampel parfum sebagai sampel yang akan diuji. berdasarkan hal tersebut, berikut data-data yang terkumpul.
|
Botol
|
Isi
|
Botol
|
Isi
|
Botol
|
Isi
|
|
1
|
102
|
11
|
97
|
21
|
101
|
|
2
|
101
|
12
|
100
|
22
|
98
|
|
3
|
98
|
13
|
98
|
23
|
100
|
|
4
|
100
|
14
|
102
|
24
|
99
|
|
5
|
101
|
15
|
99
|
25
|
102
|
|
6
|
99
|
16
|
101
|
26
|
99
|
|
7
|
98
|
17
|
98
|
27
|
101
|
|
8
|
100
|
18
|
100
|
28
|
102
|
|
9
|
102
|
19
|
101
|
29
|
101
|
|
10
|
100
|
20
|
99
|
30
|
98
|
1. Menjalankan program SPSS statistik
Pilih new di menu file. Setelah itu, pindah ke sheet ‘variabel view‘.2. Mendefinisikan data di ‘variabel view’
Pada sheet variabel view, isikan “ISI” dalam kolom pertama. Setelah itu biarkan saja dengan pengaturan default program SPSS. perhatikan gambar berikut ini.3. Mengisi data di ‘Data view’
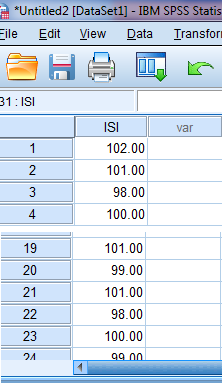
Sekarang beralihlah ke sheet ‘data view‘. lalu mulailah untuk mengisikan data yang telah terkumpul tadi ke dalam sheet tersebut. Perhatikan gambar di bawah ini.4. Melakukan pengujian sampel
Dalam melakukan pengujian menggunakan spss, ada beberapa langkah yang harus dilakukan. Berikut langkah-langkah tersebut.4.1 Pilih Analyze – compare means – one sample t test
Selanjutnya, pada bagian Menu bar, pilih Analyze > Compare Means > One Sample T Test. Perhatikan gambar di bawah ini.4.2 Dibagian sampingnya, klik ‘option’
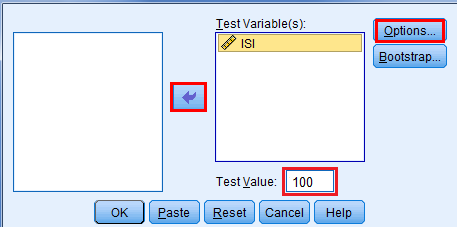
setelah itu akan muncul gambar seperti di bawah ini. Pindahkan ‘ISI’ tersebut ke sebelah kanan. Sedangkan pada bagian ‘test value‘ isikan dengan angka 100, sebab kita akan membuktikan kebenaran isi botol yang dinyatakan adalah 100 ml.
Setelah itu akan muncul tampilan seperti gambar dibawah. Pada bagian confidence interval, isi dengan 5% (nilai default). Sedangkan missing values, biarkan saja. lalu klik ‘continue‘.
5., Klik ‘OK’
Nah, setelah itu hasil pengujian akan ditampilkan pada jendela baru.6. Analisis Data
Setelah melakukan langkah-langkah pada bagian diatas, setelah itu akan muncul jendela baru yang merupakan hasil output dari pengujian yang dilakukan menggunakan SPSS statistik. Berikut hasil pengujian tersebut beserta analisisnya.A. One Sampel Statistics
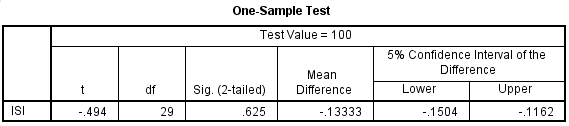
Pada output ini, terlihat ringkasan statistik dari variabel isi. Rata-rata isi botol parfum tersebut ternyata adalah 99,8667 ml, dengan standar deviasi 1,47936 ml.B. One Sample Test
Pada output ini, hipotesis yang akan di uji adalah.Ho: µ=100, Isi botol parfum tidak berbeda dengan rata-rata isi botol yang sudah ditentukan senilai 50 ml.
Ha: µ≠100, Isi botol parfum berbeda secara signifikan dengan rata-rata isi kemasan yang sudah ditentukan senilai 50 ml.
Berdasarkan hasil perhitungan, terlihat nilai t hitung adalah sebesar -0,494, bandingkan dengan nilai t tabel untuk df= 29 dan α 0,025 (pengujian 2 sisi untuk α= 5%) adalah 2,045 berarti terima Ho.
Keputusan ini juga bisa didasarkan pada probabilitas sebesar 0,625 bandingkan dengan taraf signifikan yang digunakan yaitu 0,05 yang berarti tidak signifikan.
Dengan keputusan menerima Ho berarti hipotesis bahwa isi rata-rata botol adalah 100 ml teruji. Berarti secara statistik rata-rata isi botol kemasan tidak berbeda dengan 100 ml




Tidak ada komentar:
Posting Komentar